Background
Encapsulation technologies featuring alginate hydrogels have been widely applied to the bioprocessing of food, cosmetics, pharmaceuticals, and other biomaterials. Alginate, a gelling polymer, is composed of linear polymers of 1–4 linked β-d-mannuronic acid (M) and α-l-guluronic acid (G) residues (Moe et al. 1995; Onsøyen 1997). In the presence of divalent cations such as Ca2+, alginate forms elastic hydrogels; the “egg-box” model has been adopted as a general description of alginate gel formation (Rousseau et al. 2004; Clark and Ross Murphy 1987). Alginate hydrogels have been used for the encapsulation of highly viscous high-fat food (Blandino et al. 1999), nutrients (Chen and Subirade 2006), bioactive components (Wichchukit et al. 2013), and probiotics (Subirade et al. 2010). In addition, they can protect acid-sensitive drugs from gastric fluids allowing for controlled drug release in the small intestine and are relevant to peptic ulcers (Hwang et al. 1993). Although there has been an increased number of applications of alginate hydrogels in biotechnology (Onsøyen 1996; Skjåk-bræk and Espevik 1996), studies on their use in food analogs is limited except when used as caviar (Ji et al. 2007a,b) and Cypselurus agoo roe analogs (Jo et al. 2014). Regarding the rheological characteristics of alginate hydrogels, their use in encapsulation may be a useful means of producing fish roe analogs.
Flying fish roe is one of the most consumed types of fish roes in Asia. Natural flying fish roe is widely used in sushi and for other culinary purposes in Korea and Japan. However, a consistent supply of these materials is difficult to secure due to abnormal climate changes and protective fishing policies of individual nations. Owing to this imbalance between supply and demand of these raw materials, there are limitations on their sustainable production. Therefore, the demand of suitable analogs is gradually increasing. It is also necessary to develop such analogs in order to eventually replace the natural materials, by establishing systemic processes and mass production techniques regardless of resource depletion.
In the present study, we optimize the processing conditions of these roe analogs using alginate hydrogels. The optimum conditions for production of the analogs were determined based on concentrations of sodium alginate and calcium chloride, sphericity, size, and rupture strength by using response surface methodology (RSM).
Methods
Sodium alginate and anhydrous calcium chloride (Junsei Chemical Co., Ltd., Japan) were used for gelation. All other chemicals and reagents used in this study were analytical grade.
Flying fish roe analogs were produced using a technique first reported by Jo et al. (2014), with some modifications. A sodium alginate solution was prepared at different concentrations (0.4–3.6 %, w/v) and then dropped into 0.5–2.5 % (w/v) calcium chloride at 0.06 mL/s using a peristaltic pump (Cassette tube pump SMP-23, Eyela, Japan) with a single nozzle (26G × 1/2″) connected to a silicon tube. The stirring speed of calcium chloride solution in the reactor was set at 100–500×g. The mixture was dropped every 2 min and cured for 0–60 min in solution to obtain the analogs. Afterwards, the analogs were collected with a strainer, then washed with deionized water, and stored at ambient temperature. The distance between the nozzle and the surface of the calcium chloride solution was 8 cm.
Sizes were measured according to the method of Jo et al. (2014). An image analyzer (Image-Pro program) coupled to an optical microscope (Bx-50, Olympus, Japan) was used, with image analysis at ×40 magnification. Five prepared analogs were randomly selected for each measurement and the average of their maximum and minimum diameters reported.
Sphericity was measured according to the method of Jo et al. (2014) and expressed as the percent ratio of minimum diameter to maximum diameter obtained from size measurements of the analogs.
Rupture strengths were measured according to the method of Jo et al. (2014), using a rheometer (Model CR-100D, Sun Scientific Co., Ltd., Japan) with the following conditions: round-disk stainless steel plunger 10 mm in diameter, 40 mm/min penetration speed, adapter area of 0.79 cm2, sample-adapter distance of 5 mm, and 1 kN load-cell. Five samples were measured in each experiment.
Central composite design (CCD) was adopted in the optimization of flying fish roe analog processing. The CCD in this design consists of 22 factorial points, four axial points (α = 2), and three replicates of the central point (Tables 1 and 2). Concentrations of sodium alginate (X1, %), curing time in calcium chloride solution (X2, min), calcium chloride concentration (X3, %), and calcium chloride solution stirring speed in the reactor (X4, ×g) were chosen as independent variables (IVs). The range and center point values of the four IVs were based on the results of preliminary experiments (Table 1). In order to prepare superior flying fish roe analogs in terms of external appearance, sphericity (Y1, %) was used as the dependent variable (DV). Experimental runs were randomized in order to minimize the effects of unexpected variability in the observed responses.
Y (sphericity, %), X1 (sodium alginate concentration, %), X2 (curing time in calcium chloride solution, min), X3 (calcium chloride concentration, %), X4 (rotation speed of calcium chloride solution, ×g)
The response surface methdology (RSREG procedure) of the MINITAB statistical software (Version 14, Minitab Inc., PA, USA) was used to fit the following second-order polynomial:
Here, Y is the DV, β0 is a constant, βi, βii, and βij are regression coefficients, and Xi and Xj are levels of the IVs. The response surface plots were developed using Maple software (Maple 7, Waterloo Maple Inc., Canada) and represent a function of two independent variables while keeping the other two independent variables at their optimal values.
Results and discussion
Process optimization was used to determine the conditions needed to obtain analogs most closely resembling natural ones. Sphericity, which indicates the degree of similarity between the analogs and a sphere, was defined as the ratio of minimum diameter to maximum diameter of the prepared analogs. The most important factors affecting sphericity (Y, sphericity, %) were determined in the preliminary study, with the central point and ranges determined by CCD (Box and Wilson 1951). The independent variables and central point in the analog production were the sodium alginate concentration (2 %, w/v), curing time in calcium chloride solution (30 min), calcium chloride concentration (1.5 %, w/v), and stir speed of calcium chloride in the reactor (300×g) (Table 1). A total of 27 intervals were included in the experiment, and sphericity results of the analogs prepared in each interval are shown in Table 2. RSM was performed using the data obtained by the RSREG procedure of SAS software. Based on these results, the statistical significance each associated with the linear term (X1, X2, X3, X4), quadratic term (X1X1, X2X2, X3X3, X4X4), and interaction term was determined by t-statistics. Furthermore, the statistical significance of the second-order polynomial model was measured using the estimated coefficient of each model as well as analysis of variance (ANOVA) (Table 3). For the linear coefficient, X1 (P < 0.001) and X4 (P = 0.0254) exhibited statistical significance at P < 0.05 but X2 (P = 0.0175) and X3 (P = 0.6162) did not show any statistical significance.
Y (sphericity, %), X1 (sodium alginate concentration, %), X2 (curing time in calcium chloride solution, min), X3 (calcium chloride concentration, %), X4 (rotation speed of calcium chloride, ×g)
For the quadratic coefficient, there was statistical significance found in X1X1 (P < 0.001), X3X3 (P = 0.001), and X4X4 (P = 0.020), but not X2X2 (P = 0.133). For the interaction coefficient, no significance was exhibited in X1X2 (P = 0.217), X1X3 (P = 0.993), X1X4 (P = 0.249), X2X3 (P = 0.633), X2X4 (P = 0.369), and X3X4 (P = 0.194). In order to develop fitted response surface model equations, all insignificant terms (P > 0.05) were eliminated and the resulting fitted models are shown in Table 4. The coefficient of determination in the polynomial R2 was 0.924 at P = 0.000. Such a high coefficient of determination and significance arise from experimental conditions designed by preliminary studies. ANOVA was employed to evaluate the statistical significance of the second-order polynomial model, and ANOVA based on the dependent variables was applied to express a Y (sphericity, %) response model. In the ANOVA results, all linear terms (P < 0.001) and quadratic terms (P < 0.001), except the cross-product term (P = 0.453), had probabilities >99 % (Table 5). CCD was used to identify the optimum sphericity conditions in the prepared analogs. In preliminary studies, the optimum ranges of sodium alginate concentration (X1, 2 %), curing time in calcium chloride solution (X2, 30 min), calcium chloride concentration (X3, 1.5 %), and stirring speed of the calcium chloride solution in the reactor (X4, 300 × g) were determined (Table 1). RSREG resulted in saddle points having eigenvalues that show positive and negative values. Additionally, the optimum conditions (coded values) of the analogs based on RSM were 0.51 % for the sodium alginate concentration (X1), 0.71 min for the calcium chloride solution curing time (X2), 0.02 % for calcium chloride concentration (X3), and −0.46×g for the calcium chloride solution stirring speed (X4). When these results were substituted into equation (1), X1, X2, X3, and the uncoded value of X4 were 2.41 %, 40.65 min, 1.51 %, and 254×g, respectively. When the experiment was carried out with the uncoded values as calculated above, the expected sphericity (Y, %) of the analogs was 99.9 % compared to an experimental value of 98.2 %, representing minimal difference (Table 6).
DF degrees of freedom, SS sum of square, MS mean square
X1 (sodium alginate concentration, %), X2 (curing time in calcium chloride solution, min), X3 (calcium chloride concentration, %), X4 (rotation speed of calcium chloride, ×g)
|
Factors |
Flying fish roe analogs |
Natural flying fish roe |
|---|---|---|
|
Size (mm) |
2.2 ± 0.12b |
1.88 ± 0.02a |
|
Sphericity (%) |
98.2 ± 0.2a |
98.19 ± 1.55a |
|
Rupture strength (kPa) |
762 ± 24.68a |
803.6 ± 126.37a |
The same superscripts in a raw are not significantly different each other at P < 0.05
In general, alginates undergo gelling to yield hydrogels in the presence of metallic divalent cations (Smidsrød and Haug 1972; Grant et al. 1973); for example, calcium ions make stronger alginate gels than potassium and sodium ions (Montero and Perez-Mateos 2002). When alginate solutions are added into calcium chloride solutions, calcium ions bind to the carboxylic groups of G-block alginate molecules to yield alginate gels (Moe et al. 1995; Sabraa 2005). However, M-block rich alginates have weak binding with calcium and form more elastic gels (Sabraa 2005). Alginates with high M/G ratios produce beads with smaller sizes than in the case of low M/G ratio alginate beads (Kendal Jr. et al. 2004; Mørch et al. 2006), as alginates of lower M/G ratio form more porous gels (Simpson et al. 2003). Curing of alginate gels in calcium chloride solution is promoted by increased calcium concentration, which benefits the sphericity and physical strength of the gels.
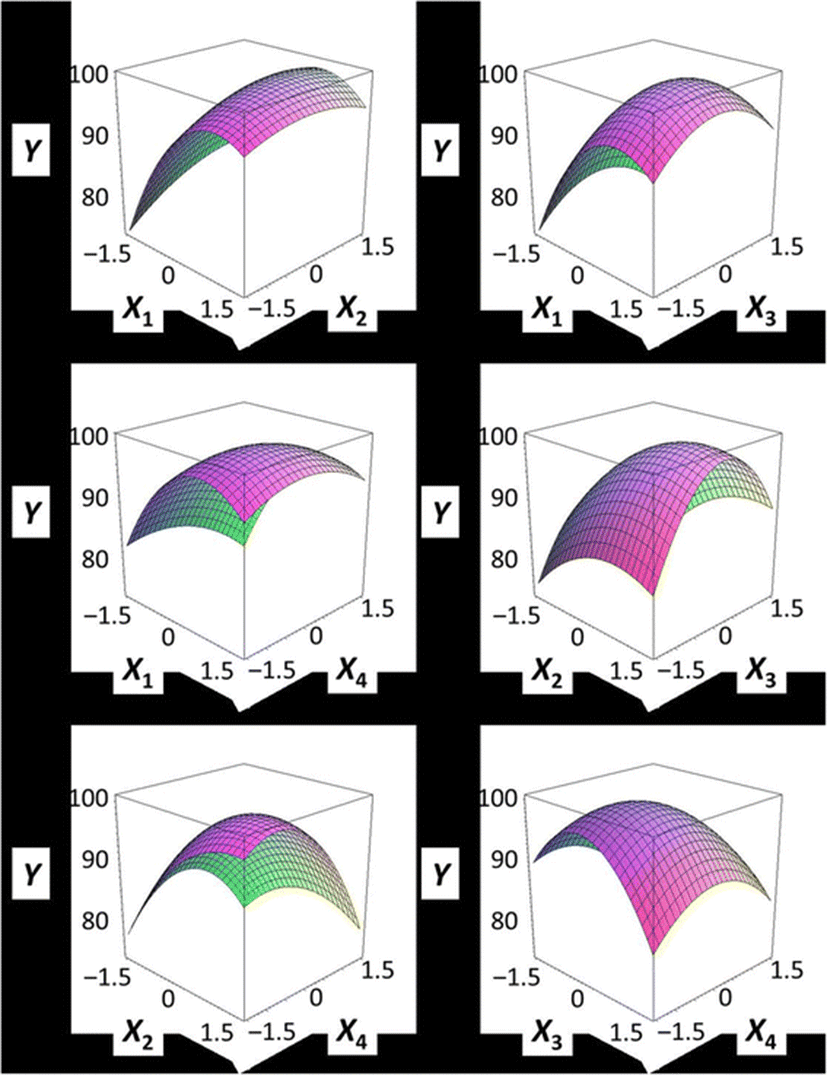
Figure 1 shows a three-dimensional graph describing the effects of the independent variables (X1, X2, X3, X4) on the dependent variable (Y) using Maple software. Among the different analog production processes, the present study focused on the effects of sodium alginate concentration (X1, %), curing time in calcium chloride solution (X2, min), calcium chloride concentration (X3, %), and calcium chloride solution stirring speed in the reactor (X4, ×g) as key factors in analog production. The graph represents the correlation between X1, X2, X3, and X4. All response surface graphs indicate that the sphericity of the analogs increased as the coded values of IVs approached zero. In particular, the sphericity of the analogs (DV) decreased remarkably as X1 approached −2. On the other hand, X2 was not considerably influential on the sphericity of the analogs compared to the other independent variables. Therefore, based on Fig. 1, all independent variables except for the curing time in calcium chloride solution influenced the sphericity of the analogs, and the concentration of sodium alginate played an especially important role. Jo et al. (2014) described the effects of heat, salt, and hydrocolloids on analog formation, and Ji et al. (2007a,b) made caviar analogs using calcium alginate gel capsules. The shape transition of the Ca-alginate beads was distinguished into three phases based on collection distance and was affected by the combined influence of the solution properties, the collection distance and the drop size (Chan et al. 2009).
Conclusions
Demand for analogs of crab meat and caviar food is gradually increasing, due to recent abnormal climate issues and fishery policy changes. Thus, improved development of such analogs is essential to substitute for natural products. Alginate was adopted for the production of flying fish roe analogs in this study because it easily forms gels and is easy to handle, non-toxic to humans, and inexpensive. The study elucidated the production of flying fish roe analogs under optimized conditions using RSM. The optimum conditions were 2.41 % sodium alginate concentration, 40.65 min curing time in calcium chloride solution, 1.51 % calcium chloride concentration, and a 254 × g stirring speed of the calcium chloride solution in the reactor. When performed at these optimum conditions, this process yielded a high sphericity of 98.2 %. The size (mm), sphericity (%), and rupture strength (kPa) of the analogs produced using these optimum conditions were 2.2 ± 0.12, 98.2 ± 0.2, and 762 ± 24.68, respectively; these physical properties are quite similar to those of natural roe. With subsequent improvements to palatability and mass production, these roe analogs may be viable substitutes for natural roe.



